Uncertainty, or experimental error, is always involved when making a measurement. If two people independently took several measurements of a physical quantity such as the weight of an object, it is unlikely that both would come up with exactly the same results every time.  Perhaps the instrument used to make the measurements is out of calibration or is influenced by variations in temperature and line voltage.  Or perhaps the instrument can’t discriminate well between two very similar values.  Or maybe personal error, carelessness, or bias is involved.  For reasons like these, measurements are never perfect; they are only approximations of some true value that is being measured.

The accuracy of a measurement refers to how close the measured values come to the true value. In other words, it is a measure of the correctness of the result.  The precision of a measurement refers to how variable the measured values are when the same quantity is measured several times. A very precise measurement would be one that did not vary much over several trials, although it may or may not be accurate.  In this section we will examine three statistics that scientists commonly use to evaluate the accuracy and precision of their measurements.

Graphing Calculator

Mean

The mean is a statistic that is used to express the “average” or “center” of a set of numbers.  When the same quantity is measured several times, the mean of the replicated measurements is a more precise measure of the quantity than any of the individual measurements.

You should have a scientific calculator that automatically calculates the mean for a list of numbers.  Use the instructions that came with your calculator to learn how to calculate the mean.  If you no longer have the instructions, you can use the instructions in Appendix B of this Manual, provided you are using the TI-36X.  If you are using a different calculator, it is fairly easy to find instructions for most calculators on the Internet (check the manufacturer’s Web site or do a Google search).  If you are still having problems, get help from one of the math tutors located in the Tutoring Labs at any ACC campus.

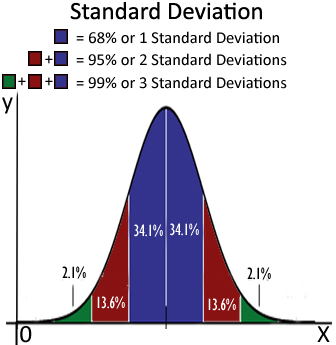Standard Deviation – used to express precision

Precision refers to how close replicate measurements are to each other.  It is often expressed in terms of the standard deviation.  In general, the less variation there is among the values, the lower the standard deviation, and the better the precision of the measurements.

Use the instructions that came with your calculator to learn how to calculate standard deviation.  If you no longer have the instructions, you can use the instructions in Appendix B of this Manual, provided you are using the TI-36X.  If you are using a different calculator, you can find instructions for most calculators on the Internet (check the manufacturer’s Web site or do a Google search).  If you are still having problems, get help from one of the math tutors located in the Tutoring Labs at any ACC campus.

NOTE: Make sure you use the correct units and the correct number of significant digits in all of your answers below.

A student uses a 100 mL beaker to measure 80.0 mL of deionized water (dH₂O).  She then weighs the water with an electronic balance.  Following this procedure 6 times, she obtains the following results:  82.89 g, 80.23 g, 81.27 g, 81.92 g, 82.03 g, and 80.17 g. 

1. Enter the mean volume of water delivered by the 100 mL beaker in the space provided.

2. Enter the percent error of the mean for the volumes of water delivered by the beaker.

3. Enter the standard deviation (σ_{x n – 1}) for the volumes of water delivered by the beaker.

Check your answers:

1. Mean (= 81.42 mL)

2. % error (= 1.78%)

3. Standard Deviation (= 1.08 mL)

During the second part of her experiment, the student repeats her measurements using a 100 mL graduated cylinder instead of a beaker.  This time she obtains the following results: 80.79 g, 79.33 g, 80.25 g, 79.82 g, 80.13 g, and 80.19 g. 

1. Enter  the mean volume of water delivered by the 100 mL graduated cylinder in the space provided.

2. Enter the percent error of the mean for the volumes of water delivered by the graduated cylinder.

3. Enter the standard deviation (σ_{x n – 1}) for the volumes of water delivered by the graduated cylinder.

Check your answers:

1. Mean (= 80.09 mL)

2. % error (= 0.1%)

3. Standard Deviation (= 0.49 mL)

Which measuring device seems to be more accurate? Explain your answer.

  (Check your answer.) (Recall that percent error of the mean measures accuracy. The closer the measured values are to the desired value, the smaller the percent error of the mean, and the greater the accuracy of the measurements. In this case, the percent error for the beaker is 1.78% while that of the cylinder is 0.1%. Therefore, the results indicate that the 100 mL cylinder is more accurate for measuring 80 mL of water.)

(Check your answer.) (Recall that standard deviation measures precision. A smaller SD indicates less variation among the measurements and, therefore, greater consistency or precision. In this case, the SD for the beaker is 1.08 mL while that of the cylinder is 0.49 mL. Therefore, the results indicate that the 100 mL cylinder is more precise for measuring 80 mL of water.)

• For the beaker, the numerator calculation was 81.42 g - 80.00 g = 1.42 g. This number has 3 significant digits and so the percent error has 3 significant digit.
• For the cylinder, the numerator calculation was 80.09 g - 80.00 g = 0.09 g. This number has only 1 significant digit, so the percent error has only 1 significant digit.