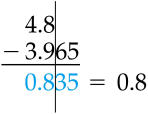
BIOL 1406
PreLab 1.9
When reporting a computed value, how many significant digits should I use?
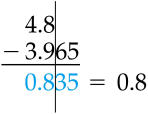 |
Calculations performed on measurements often produce results with more digits than the original measurements. Suppose, for example, that you use a calculator to determine the average of 3.0, 3.2, 3.3, 3.2, and 3.1 mm, and the result displayed on the calculator is 3.13333 mm. This number implies that the average is accurate to within a hundred thousandth of a millimeter! Unfortunately, your data does not become more accurate simply because you carried out a series of calculations. Therefore, computed values should not have more significant digits than the original data. In this example, the average should be rounded off to 3.1 mm. |
When you multiply or divide, your answer should have the same number of significant digits as the number with the fewest. For example, if you want to calculate the volume of a cube by multiplying the length of its sides, it might look like this:
(3.4 mm) x (56.8 mm) x (2.435 mm) = 470.2472 mm3 (on your calculator)
However, the answer you report should have the same number of significant digits as the measurement with the fewest (3.4 mm), so you should only report 2 significant figures: 4.7 x 102 mm3.
The rules change when you are adding or subtracting numbers. In this case, you look at the number of decimal places to determine the accuracy of the measurement. The final answer can have no more digits to the right of the decimal than the number involved in the operation with the fewest digits to the right of its decimal. For example, if you are adding volumes to get a total, it might look like this:
(2.4 mL) + (351 mL) + (0.543 mL) = 353.943 mL (on your calculator)
If you look at the decimal places, however, you will notice that the 351 mL measurement has no digits to the right of the decimal. Therefore, you should report the total volume as 354 mL.
| Your Turn | ||
| Calculate the answer to the following problem and express your answer with the correct units and the correct number of significant digits. | ||
| (34.0 g x 0.003 g) ∕ (1.90 g x 20.0 g) = | Hint | Check your answer. |
| Calculate the answer to the following problem and express your answer with the correct units and the correct number of significant digits. | ||
| 12.098 g - 11.6 g = | Hint | Check your answer. |
Close this browser window to return to Blackboard and complete the practice quiz and assessment quiz.